R Plots Not Showing

• R Plot Title Not Showing
• R Shiny Plot Not Showing
• R Markdown Plots Not Showing
• R Plots Not Showing Random

I tried tools global options panes plots is selected. I don't know what other info to share. I can see the plot pane with 'plots' tab active. Screen: Notice the new menu with 'Quartz' appear. Not sure what this is, but it comes up when R generates the plot and the usual RStudio menu disappears. It’s not always easy getting the right size. The image is CC by Kristina Gill. A vital part of statistics is producing nice plots, an area where R is outstanding. The graphical ablility of R is often listed as a major reason for choosing the language. It is therefore funny that exporting these plots is such an issue in Windows. R par function. We can put multiple graphs in a single plot by setting some graphical parameters with the help of par function. R programming has a lot of graphical parameters which control the way our graphs are displayed. The par function helps us in setting or inquiring about these parameters. For example, you can look at all the.

If you find this page useful, and want more of the same, try our hyperbook

Why spanners? Since 'throwing a spanner into the works' has bad connotations, let us begin with the most popular, normal, conventional (if blunt) tool.

Histograms / bargraphs

Unless you are trying to show data do not 'significantly' differ from 'normal' (e.g. using Lilliefors test) most people find the best way to explore data is some sort of graph. Yet, whilst there are many ways to graph frequency distributions, very few are in common use. Journalists (for reasons of their own) usually prefer pie-graphs, whereas scientists and high-school students conventionally use histograms, (or bar-graphs). Curiously, while statisticians condemn pie-graphs as misleading if not wholly inappropriate, they seldom criticise histograms - at any rate histograms appear in virtually every introductory statistics text, and many advanced ones.

When asked to examine a distribution most people assume they are merely being asked to look at a histogram (which seldom stirs much enthusiasm) either before or after performing a statistical analysis. One justification (noted elsewhere) is publishers are reluctant to 'waste' page space upon qualitative and basic exploration. A more practical reason is that histograms work well when applied to very large sets of normal values, but are not a good way to examine small sets of values, or especially non-normal data. This is partly because, whilst grouping values into class-intervals smooths their distribution to some extent, that smoothing is wholly arbitrary. When applied to values which are highly skewed, highly polymodal, or highly discrete the outcome wholly depends upon your choice of breakpoints (even if you are unaware of making that choice).

If you assume R's default settings are liable to be the most reasonable in most circumstances, plotting a histogram is almost childishly simple. But, when inspecting a histogram, do remember that genuinely normal values are smoothly distributed.

The following code instructs R to randomly select a large sample of (n=1000000) values from a standard normal population and put ('assign') those values in a variable called 'y', then plot a histogram thereof.

n = 1000000 # set the sample size p = runif(n) # randomly select n values of p y = qnorm(p) # give n standard normal quantiles hist(y) # do a histogram of y using R's defaults

Note:
• because our intention is not to provide a software library, but to illustrate principles and promote thought, we only provide the most minimal R-code here.
• In the interests of clarity, we annotated our graphs using a simple image editor (MS PCpaint).
• For those new to R, text to the right of a hashmark is for your information, not R's.
• R purists may be horrified that we often assign values to variables using rather than

Histograms perform tolerably well when 'sensibly' applied to very large samples of 'normal' data, but very poorly when obtained from small samples and/or particularly non-normal data.

There are two obvious reasons for that:
1. The choice of class intervals is almost always arbitrary, hence prone to artefacts and bias.
2. Collapsing data to class-intervals, equally arbitrarily, discards fine-structure information.

Of course, if a sample distribution's fine-structure is solely due to simple random variation, smoothing this out can give a more realistic picture of the population that sample represents. But that is only true if the smoothing function is appropriate! Which is one reason why histograms can be astonishingly misleading when their breakpoints are poorly (or unluckily) chosen.

Let us therefore consider some other ways of graphically displaying how values are distributed which do not require class-intervals.

Surprisingly, the rank-based nonparametric viewpoint has much to offer in exploring distributions - even if you merely want to see whether re-scaling (transforming) your data has made its errors roughly normal.

Unfortunately, for historical reasons, it is commonly assumed that is the only reason to examine a distribution.

Some of the most useful procedures were devised for sampling distributions, or as extensions of confidence intervals, but are seldom applied to the actual data.

Univariate scatterplots

For a variety of reasons, univariate scatterplots (rugplots) are the simplest way to compare how sets of values are distributed - yet they are surprisingly rarely used, even in elementary stats texts. By convention rugplots are plotted along one or more of a graph's axes, often the x-axis, hence its name (imagine a rug viewed edge-on) - but this need not be so.

Therefore, whilst R's function allows you to add a rugplot to an existing plot, the following code takes a sample of n observations from a defined population (Y), and plots them as a simple (vertical) rugplot.

n=100 # this defines the sample size # now we set up a small population of values Y=c(1,4,2,5,1,7,3,8,11,0,19) y=sample(Y,n,replace=TRUE) # then take a random sample # display the contents of y as a rugplot x=rep(1,n) # arbitrarily, set ALL x=1 plot(x, y) # plot y against 1

• Note that this graph represents (n=) 100 values - yet only 10 are visible on the plot. This is because y can only take the value of one of the ten discrete values given above. Tied values are not distinguished.

The following code requests R to take three random samples of different 'theoretical' populations, then to plot them as 'rugplots' up the middle of a graph. This time we have used dashes to minimize point overlap.

# first we sample 3 different populations n1=200; y1=rnorm(n1,3,1) n2=100; y2=runif(n2,0,6) n3=50; y3=rlnorm(n3)/3 # arbitrarily set an x-value for each variable x1=rep(1,n1) x2=rep(2,n2) x3=rep(3,n3) # plot 3 univariate scatterplots (rugplots) plot(x1,y1, pch='-', xlim=range(x1,x2,x3), ylim=range(y1,y2,y3)) points(x2,y2, pch='-', col='blue') points(x3,y3, pch='-', col='red')

• Since we believe computers should be machines which save us work, we often disregard convention and use rather than
• Similarly, given R provides 'random' theoretical functions, we thought might be clearer than , and have used rather than

Conventional dotplots

Dotplots, traditionally drawn with graphpaper and pen, used to be a popular way to display distributions of small, heavily tied, sets of values.

The R code below assigns some values to a variable (y), then plots a conventional dotplot, with duplicate values arranged evenly above and below.

y=c(445,530,540,510,570,530,545,545,505,535,450,500, 520,460,430,520,520,430,535,535,475,545,420,495, 485,570,480,495,470,490) x=rank(y,ties.method='first') - rank(y,ties.method='average') plot(y, x, ylab=')

The conventional way to go about this task was (to instruct some unfortunate technician) to plot values initially as a rugplot, adding tied-values alternately above and below their fellows. Provided each value has an odd number of tied values the graph should be symmetrical about the x-axis, otherwise the result was arbitrarily assymetric - and for large sets of values, a tedious, untidy, and unsatisfactory affair.

Conventional dotplots display tied values one above the other. They are also known as univariate scatterplots, dot histograms or histogram-type dotplots, or (along with jittered dotplots) as density plots. Another form of dot histogram displays tied values by plotting the frequency of ties of each value of y, on the value of y, as described below.

Jittered dotplots

One advantage of those very simple (univariate) plots is that even an untrained eye can readily interpret the differing densities of values - until, that is, the points overlap. Therefore, whilst rugplots have an attractive simplicity for very small sets of values, they do not cope well with high densities of similar values, or with 'tied', 'discrete' data.

Years before computers were available, a popular way around those constraints was to plot the values as dotplots using ordinary graphpaper and, if there were duplicate or very-similar values, to add them (more-or-less evenly) either side of those already plotted. Given which, the wider the dotplot, the denser the values were around that value. Statisticians have criticised this method, partly because the rules for adding points were not standard, but especially because it has a habit of introducing unwanted, arbitrary, and sometimes misleading patterning.

Now computers are ubiquitous, and we have good pseudo-random-number algorithms, an increasingly popular way to separate similar values, whilst not introducing bias, is to add uniformly-distributed random variation orthogonally (at-right angles, or 90 degrees) to the observed values. Since adding random variation is known as 'jittering', these are commonly known as jittered dotplots, or jittered scatterplots.

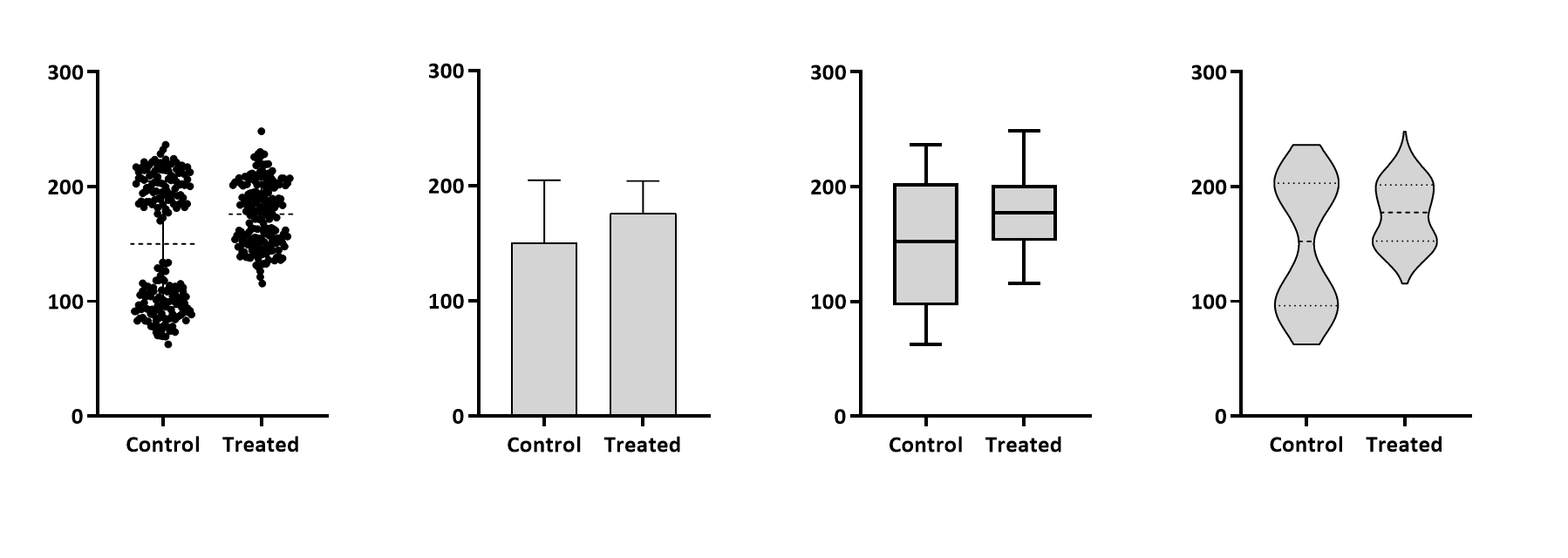
The R code for displaying a single sample as a jittered dotplot is gloriously simple. The following code displays the sample obtained above

n=100 # this defined the sample size # we then set up a small population of values Y=c(1,4,2,5,1,7,3,8,11,0,19) y=sample(Y,n,replace=TRUE) # then took a random sample x=runif(n) # assign uniform random errors to x plot(y, x) # do a jittered dotplot of x on y

• Note the jittering variation (provided by the function) is uniformly, not normally distributed - in other words the jittering value is equally likely to have any value from zero to one (so uniform populations are usually parameterized by a minimum and maximum, rather than a mean and standard deviation).
• Notice also that, entirely for our own convenience, we plotted the y-variable horizontally rather than vertically.

Smoothing distributions

Applying repeated random variation to the observed values themselves, then averaging the result, smooths their distribution. But, if the result is not to be misleading, this smoothing requires you select suitably-distributed error-distribution, e.g. normal.

The following code instructs R to apply Gaussian (normal) smoothing to the values in variable y3, and plot their mean probability density. We have added the original values as a rugplot.

# this was how we got y3 n3=50; y3=rlnorm(n3)/3 plot(density(y3)) rug(y3, col='red') # add a rugplot of y3

The computational advantage of using a theoretical and mathematically-defined function is you do not have to repeatedly jitter all your sample values, then examine how the jittered vales are distributed.

The advantage to users is smoothed plots resemble theoretical plots and histograms in text-books.

Since the form and degree of smoothing is unavoidably arbitrary, every smoothing function risks introducing bias and artefacts - even if that smoothing function is a simple running mean, or class-intervals (as used in histograms). Jittered scatterplots do not introduce bias on average, but when jittering is applied to an individual sample the human eye smooths the distribution to a random hence uneven degree.

The following code instructs R to produce jittered scatterplots of the 3 samples above

# this is how we obtained y1 y2 y3 n1=200; y1=rnorm(n1,3,1) n2=100; y2=runif(n2,0,6) n3=50; y3=rlnorm(n3)/3 # jitter the x-values x1=runif(n1) x2=runif(n2)+2 x3=runif(n3)+4 # then plot each y on x plot(x1,y1, pch='+', xlim=range(x1,x2,x3), ylim=range(y1,y2,y3)) points(x2,y2, pch='+', col='blue') points(x3,y3, pch='+', col='red')

One important limitation of rugplots, jittered dotplots and their ilk, is they tend to obscure any fine structure within a sample distribution, such as tied values, or patterns within very similar values. Ironically, whilst many nonparametric statistics collapse data to ranks, rank-based methods avoid the problems inherent to class-intervals, and can retain all the fine structure for examination.

Simple rank scatterplots

Arguably the simplest rank-based graphical technique is a scatterplot of rank on value.

For instance, the following code instructs R to randomly select (n=) 30 values from a defined population distribution, and show the result as a scatterplot of rank on value.

n=30 y=10^round(rnorm(n)) plot(sort(y), 1:n)

Remember, with all the plots on this page, you are unlikely to get precisely (or sometimes even approximately) the same result as us, because the values are selected at random!

You can get the same result using these instructions:

plot(y, rank(y,ties.method='random'))

• In the interest of readability, we decided not to reduce to

Notice that, because R's function assumes you want the mean (average, or expected) rank of tied values, the following code would loose some of that valuable information - unless the data lacks ties (so every value is unique) - which often happens in small samples, even of highly-discrete populations.

# this was how we got y n=30 ; y=10^round(rnorm(n)) plot(y, rank(y))

Notice this plot tends to obscure how ties within the data are distributed.

Cumulative rank scatterplots

If you wish to compare several samples containing unequal numbers of values it helps to standardize the ranks - most simply by converting to relative rank - as in this example:

# take THREE samples of ONE population: n1=30 ; y1=rnorm(n1) # this takes sample # 1 n2=20 ; y2=rnorm(n2) # this takes sample # 2 n3=10 ; y3=rnorm(n3) # this takes sample # 3 n=n1 ; y=y1 # for sample #1 p=rank(y,ties='random')/n # this ranks y plot(y, p) # plot p on y n=n2 ; y=y2 # for sample #2 p=rank(y,ties='random')/n # this ranks y points(y, p,col='blue') # add this plot n=n3 ; y=y3 # for sample #3 p=rank(y,ties='random')/n # this ranks y points(y, p, col='red') # add this plot

• When relative rank is calculated in that way (p = r/n), for any given value, p is the proportion of values in y whose ranks are less than or equal to that value - hence ranking is a cumulative function (re-mapping).

These plots are also known as empirical distributions functions (ECDF), and to emphasize the fact they are unavoidably discrete, they are often plotted as stepplots. Plotting them as lineplots smooths the distribution to the eye, and makes them easier to compare, but implicitly assumes intermediate values could realistically be observed.

If you want to use R's ECDF function, you can plot the results using

Theoretical statisticians might also point out that an ECDF provides a maximum-likelihood estimate (MLE) of the population's cumulative distribution function (CDF) - and note that many MLE's are biased. In more everyday terms, these plots are cumulative distributions. Unfortunately, owing to the way statistics are taught in schools, the histogram holds powerful sway, and most people find cumulative distributions comparatively hard to interpret.

P-value plots

One reason cumulative distributions are unpopular is because people find it hard judge their location, dispersion, or skew. A simple way to address these issues is to use convert values of p above 0.5 to 1 minus p - in other words to reflect the upper tail downwards. However, since 1/n >= r/n >= 1 is inherently assymetric, p = {r-0.5}/n is a less biased measure of relative rank.

The following code takes 3 samples in the same way as immediately above, then presents them as p-value lineplots - to aid comparison, a vertical line shows each sample median.

n1=30 ; y1=rnorm(n1) # sample #1 n2=20 ; y2=rnorm(n2) # sample #2 n3=10 ; y3=rnorm(n3) # sample #3 n=n1;y=y1 # for sample #1 p=.5:n/n # p value = (r-0.5)/n p=abs((p>.5)-p) # if p > 0.5 then p = 1-p plot(sort(y),p, type='l') # y=y1 abline(v=median(y)) n=n2;y=y2 # for sample #2 p=.5:n/n # P value = (r-0.5)/n p=abs((p>.5)-p) # if p > 0.5 then p = 1-p points(sort(y),p, type='l', col='blue') # y=y2 abline(v=median(y), col='blue') n=n3;y=y3 # for sample #3 p=.5:n/n # P value = (r-0.5)/n p=abs((p>.5)-p) # if p > 0.5 then p = 1-p points(sort(y),p, type='l', col='red') # y=y3 abline(v=median(y), col='red')

One disadvantage of p-value plots is, since they are seldom used, they confuse the uninitiated - including otherwise-sensible statisticians.

• The p-values in these examples employ sample quantiles (not theoretical quantiles) so must not be confused with P-values of test statistics, or P-value plots of nested confidence intervals.
• Since no-one refers to 'empirical QQ plots', talking about 'empirical p-value plots' seems unlikely to improve matters.

Frequency of ties

One advantage of rank scatterplots is that, being cumulative, they are less affected by fine structure than rank-frequency plots - the larger your sample size, the less variable is its cumulative distribution. Hence the peak of each p-value plot (the median is where p=0.5) is a more reliable measure of location than a histogram's mode.

The following code instructs R to plot the relative frequency of each value of y1, calculated from its rank. Bars indicate the frequency each value is tied + 1.

# this is how we obtained y3 n1=30 ; y1=rnorm(n)) f=rank(y1, ties='max')-rank(y1, ties='min')+1 plot(y1,f, type='h') # for relative frequency use f/n instead of f abline(0,0)

Of course unless they are subject to rounding, because a normal population contains an infinite number of different values, the probability of selecting two identical normal values by chance approaches zero. In which case the frequency distribution (for example see above) is polymodal, therefore every mode has the same height (f = 1), and the result is equivalent to a univariate plot or rugplot. Rounded large samples produce histogram-like results - but, if the rounding is uneven, such plots are misleading. Remember, given sufficiently many class-intervals, a histogram will also have up to n modes, unless values are tied - in which case the result is equivalent to a bargraph.

At the opposite extreme, most people assume straight lines must be relatively easy to appraise. Which may explain why quantile-quantile plots (QQ plots) are a relatively popular way to compare two distributions.

Q-Q plots

The following instructions are a simple and transparent way to compare two samples of equal size:

n=30 y1=rnorm(n) # sample #1 y2=rnorm(n) # sample #2 plot(sort(y1),sort(y2)) # show expected relationship abline(0,1) # if Y1=Y2

A few moments thought reveals that if both samples are of the same population we would expect, on average, a QQ plot's points will be identical. Whereas, if the values are selected at random, this will seldom occur - unless the population is extremely small indeed. If you compare two large samples of infinite normal populations, you commonly find values are very similar around the plot's center, but differ at its extremes.

If your samples are of unequal size, R's function can use interpolated values from the larger sample. So if y1 has 3000 values and y2 has 3 values, qqplot only produces 3 points.

Normal quantile plots

Because two-sample QQ plots are comparatively rare, most people assume QQ plots are only used to see if a set of values deviates from their expected ('theoretical') normal values. This type of plot is more correctly termed a normal quantile plot, for example as follows:

n=7; y=rnorm(n) # select n values from a normal population P=.5:n/n plot(qnorm(P), sort(y))

• Notice that in real data the normal population's mean and standard deviation are seldom known, unless they are standardized (e.g. using ), these quantiles will be linearly related, but unequal.
• Again, because the theoretical values are normal population quantiles, a relative rank of P=r/n would bias those theoretical values. So, to reduce that bias, we use (r-0.5)/n
  For instance in a sample of n values the highest possible rank (r_max) equals n, therefore r_max/n = 1. However, if y is randomly selected from a normal distribution, we are unlikely to observe the highest value of y is infinite - unless n is also infinite.
  Other corrections are available to reduce the bias further, nevertheless the extreme points of small samples of normal populations should be expected to slightly deviate from a linear relationship.

Two further alternatives

If you prefer to use R's normal quantile function, it is called

The following code applies R's normal quantile function to the expected values of 5 normal observations, which we estimate from (R=) 50000 random samples (of n=15 values) from a normal population (otherwise known as ranked normal deviates, or rankits).

# estimate the values of n rankits n=15 ; R=50000 # put Rn random normal values in a matrix Y=matrix(rnorm(n*R), ncol=R) Y=apply(Y,2,sort) # sort each sample Y=apply(Y,1,mean) # average the sorted values # the n rankits in Y are 'observed' qqnorm(Y, pch='+') # R finds their 'theoretical' values

Lest you assume theoretical quantiles estimated via simulation (such as rankits) have no advantage over theoretical quantiles obtained from an inverse probability function, let us compare them a little more carefully.

The following code asks R to plot the difference between the (estimated) expected values on their theoretical quantiles (in this case obtained R's normal quantile plot function). Plotting the deviations from expected against their observed values is much more sensitive than a simple QQ plot - so can reveal systematic differences in two otherwise similar distributions.

# this was how we estimated n rankits n=15 ; R=50000 # put R*n random normal values in a matrix Y=matrix(rnorm(n*R), ncol=R) Y=apply(Y,2,sort) # sort each sample Y=apply(Y,1,mean) # average the sorted values q=qqnorm(Y, plot=FALSE) plot(q$x, q$y-q$x) abline(0,0)

• Notice that the median value is unbiased.
• In this example Y contained standard rankits, because their values are similar to theoretical standard normal quantiles.
• For a real sample, because the population parameters are unknown, you would only expect no difference if the data were standardized prior to plotting, for example using:

See also

More examples of R code for displaying frequency distrbutions: Drawing a histogram, a frequency polygon, a stem and leaf plot, jittered dot plot, rank scatterplots, frequency of each value, empirical cumulative distribution function (ECDF), P-value plot, multiple P-value plots, smoothed distribution function.

Elementary Statistics (Pages of information about basic statistics - for struggling Students - and their teachers): Displaying frequency distributions + Means, medians, modes + Types of variables + Variance and Standard Deviation + Standard error of the mean + The Normal distribution + Relationships between variables + Quantiles (median, range, interquartile and 90% range) + Statistics for beginners (using R) + Extras (where values are not normal)

This tutorial uses ggplot2 to create customized plots of time series data. We will learn how to adjust x- and y-axis ticks using the scalespackage, how to add trend lines to a scatter plot and how to customize plotlabels, colors and overall plot appearance using ggthemes.

Learning Objectives

After completing this tutorial, you will be able to:

• Create basic time series plots using ggplot() in R.
• Explain the syntax of ggplot() and know how to find out more about thepackage.
• Plot data using scatter and bar plots.

Things You’ll Need To Complete This Tutorial

You will need the most current version of R and, preferably, RStudio loaded onyour computer to complete this tutorial.

Install R Packages

• lubridate:install.packages('lubridate')
• ggplot2:install.packages('ggplot2')
• scales:install.packages('scales')
• gridExtra:install.packages('gridExtra')
• ggthemes:install.packages('ggthemes')

More on Packages in R – Adapted from Software Carpentry.

Download Data

NEON Teaching Data Subset: Meteorological Data for Harvard Forest

The data used in this lesson were collected at the National Ecological Observatory Network's Harvard Forest field site. These data are proxy data for what will be available for 30 years on the NEON data portalfor the Harvard Forest and other field sites located across the United States.

Set Working Directory: This lesson assumes that you have set your working directory to the location of the downloaded and unzipped data subsets.

R Script & Challenge Code: NEON data lessons often contain challenges that reinforce learned skills. If available, the code for challenge solutions is found in thedownloadable R script of the entire lesson, available in the footer of each lesson page.

Additional Resources

• Winston Chang'sCookbook for R site based on his R Graphics Cookbook text.
• The NEON Data Skills tutorial on Interactive Data Viz Using R, ggplot2 and PLOTLY.
• Data Carpentry's Data Visualization with ggplot2 lesson.
• Hadley Wickham's documentation on the ggplot2 package.

Plotting Time Series Data

Plotting our data allows us to quickly see general patterns including outlier points and trends. Plots are also a useful way to communicate the results of our research. ggplot2 is a powerful R package that we use to create customized, professional plots.

Load the Data

We will use the lubridate, ggplot2, scales and gridExtra packages inthis tutorial.

Our data subset will be the daily meteorology data for 2009-2011 for the NEONHarvard Forest field site(NEON-DS-Met-Time-Series/HARV/FisherTower-Met/Met_HARV_Daily_2009_2011.csv).If this subset is not already loaded, please load it now.

Plot with qplot

We can use the qplot() function in the ggplot2 package to quickly plot avariable such as air temperature (airt) across all three years of our dailyaverage time series data.

The resulting plot displays the pattern of air temperature increasing and decreasing over three years. While qplot() is a quick way to plot data, our ability to customize the output is limited.

Plot with ggplot

The ggplot() function within the ggplot2 package gives us more controlover plot appearance. However, to use ggplot we need to learn a slightly different syntax. Three basic elements are needed for ggplot() to work:

1. The data_frame: containing the variables that we wish to plot,
2. aes (aesthetics): which denotes which variables will map to the x-, y-(and other) axes,
3. geom_XXXX (geometry): which defines the data's graphical representation(e.g. points (geom_point), bars (geom_bar), lines (geom_line), etc).

The syntax begins with the base statement that includes the data_frame(harMetDaily.09.11) and associated x (date) and y (airt) variables to beplotted:

ggplot(harMetDaily.09.11, aes(date, airt))

To successfully plot, the last piece that is needed is the geometry type. In this case, we want to create a scatterplot so we can add + geom_point().

Let's create an air temperature scatterplot.

Customize A Scatterplot

We can customize our plot in many ways. For instance, we can change the size and color of the points using size=, shape pch=, and color= in the geom_pointelement.

geom_point(na.rm=TRUE, color='blue', size=1)

Modify Title & Axis Labels

We can modify plot attributes by adding elements using the + symbol.For example, we can add a title by using + ggtitle='TEXT', and axislabels using + xlab('TEXT') + ylab('TEXT').

Data Tip: Use help(ggplot2) to review the manyelements that can be defined and added to a ggplot2 plot.

Name Plot Objects

We can create a ggplot object by assigning our plot to an object name.When we do this, the plot will not render automatically. To render the plot, weneed to call it in the code.

Assigning plots to an R object allows us to effectively add on to, and modify the plot later. Let's create a new plot and call it AirTempDaily.

Format Dates in Axis Labels

We can adjust the date display format (e.g. 2009-07 vs. Jul 09) and the number of major and minor ticks for axis date values using scale_x_date. Let'sformat the axis ticks so they read 'month year' (%b %y). To do this, we will use the syntax:

scale_x_date(labels=date_format('%b %y')

Rather than re-coding the entire plot, we can add the scale_x_date elementto the plot object AirTempDaily that we just created.

Data Tip: You can type ?strptime into the R console to find a list of date format conversion specifications (e.g. %b = month).Type scale_x_date for a list of parameters that allow you to format dates on the x-axis.

Data Tip: If you are working with a date & timeclass (e.g. POSIXct), you can use scale_x_datetime instead of scale_x_date.

Adjust Date Ticks

We can adjust the date ticks too. In this instance, having 1 tick per year may be enough. If we have the scales package loaded, we can use breaks=date_breaks('1 year') within the scale_x_date element to create a tick for every year. We can adjust this as needed (e.g. 10 days, 30 days, 1 month).

From R HELP (?date_breaks): width an interval specification, one of 'sec', 'min', 'hour', 'day', 'week', 'month', 'year'. Can be by an integer and a space, or followed by 's'.

Data Tip: We can adjust the tick spacing andformat for x- and y-axes using scale_x_continuous or scale_y_continuous toformat a continue variable. Check out ?scale_x_ (tab complete to view the various x and y scale options)

ggplot - Subset by Time

Sometimes we want to scale the x- or y-axis to a particular time subset without subsetting the entire data_frame. To do this, we can define start and end times. We can then define the limits in the scale_x_date object as follows:

scale_x_date(limits=start.end) +

ggplot() Themes

We can use the theme() element to adjust figure elements.There are some nice pre-defined themes that we can use as a starting place.

Using the theme_bw() we now have a white background rather than grey.

Import New Themes BonusTopic

There are externally developed themes built by the R community that are worthmentioning. Feel free to experiment with the code below to install ggthemes.

More on Themes

Customize ggplot Themes

We can customize theme elements manually too. Let's customize the font size and style.

Challenge: Plot Total Daily Precipitation

Create a plot of total daily precipitation using data in the harMetDaily.09.11data_frame.

• Format the dates on the x-axis: Month-Year.
• Create a plot object called PrecipDaily.
• Be sure to add an appropriate title in addition to x and y axis labels.
• Increase the font size of the plot text and adjust the number of ticks on thex-axis.

Bar Plots with ggplot

We can use ggplot to create bar plots too. Let's create a bar plot of total daily precipitation next. A bar plot might be a better way to represent a totaldaily value. To create a bar plot, we change the geom element fromgeom_point() to geom_bar().

The default setting for a ggplot bar plot - geom_bar() - is a histogramdesignated by stat='bin'. However, in this case, we want to plot actualprecipitation values. We can use geom_bar(stat='identity') to force ggplot toplot actual values.

Note that some of the bars in the resulting plot appear grey rather than black.This is because R will do it's best to adjust colors of bars that are closelyspaced to improve readability. If we zoom into the plot, all of the bars areblack.

Challenge: Plot with scale_x_data()

Without creating a subsetted dataframe, plot the precipitation data for 2010 only. Customize the plot with:

• a descriptive title and axis labels,
• breaks every 4 months, and
• x-axis labels as only the full month (spelled out).

HINT: you will need to rebuild the precipitation plot as you will have to specify a new scale_x_data() element.

Bonus: Style your plot with a ggtheme of choice.

Color

We can change the bar fill color by within thegeom_bar(colour='blue') element. We can also specify a separate fill and linecolor using fill= and line=. Colors can be specified by name (e.g., 'blue') or hexadecimal color codes (e.g, #FF9999).

There are many color cheatsheets out there to help with color selection!

Data Tip: For more information on color,including color blind friendly color palettes, checkout the ggplot2 color information from Winston Chang's CookbookforR site based on the RGraphicsCookbook text.

Figures with Lines

We can create line plots too using ggplot. To do this, we use geom_line()instead of bar or point.

Note that lines may not be the best way to represent air temperature data givenlines suggest that the connecting points are directly related. It is importantto consider what type of plot best represents the type of data that you arepresenting.

Challenge: Combine Points & Lines

You can combine geometries within one plot. For example, you can have ageom_line() and geom_point element in a plot. Add geom_line(na.rm=TRUE) tothe AirTempDaily, a geom_point plot. What happens?

Trend Lines

We can add a trend line, which is a statistical transformation of our data torepresent general patterns, using stat_smooth(). stat_smooth() requires astatistical method as follows:

• For data with < 1000 observations: the default model is a loess model(a non-parametric regression model)
• For data with > 1,000 observations: the default model is a GAM (a generaladditive model)
• A specific model/method can also be specified: for example, a linear regression (method='lm').

R Plot Title Not Showing

For this tutorial, we will use the default trend line model. The gam method will be used with given we have 1,095 measurements.

Data Tip: Remember a trend line is a statisticaltransformation of the data, so prior to adding the line one must understand if a particular statistical transformation is appropriate for the data.

Challenge: A Trend in Precipitation?

R Shiny Plot Not Showing

Create a bar plot of total daily precipitation. Add a:

• Trend line for total daily precipitation.
• Make the bars purple (or your favorite color!).
• Make the trend line grey (or your other favorite color).
• Adjust the tick spacing and format the dates to appear as 'Jan 2009'.
• Render the title in italics.

Challenge: Plot Monthly Air Temperature

Plot the monthly air temperature across 2009-2011 using theharTemp.monthly.09.11 data_frame. Name your plot 'AirTempMonthly'. Be sure tolabel axes and adjust the plot ticks as you see fit.

Display Multiple Figures in Same Panel

It is often useful to arrange plots in a panel rather than displaying them individually. In base R, we use par(mfrow=()) to accomplish this. Howeverthe grid.arrange() function from the gridExtra package provides a moreefficient approach!

R Markdown Plots Not Showing

grid.arrange requires 2 things:1. the names of the plots that you wish to render in the panel.2. the number of columns (ncol).

grid.arrange(plotOne, plotTwo, ncol=1)

Let's plot AirTempMonthly and AirTempDaily on top of each other. To do this,we'll specify one column.

Challenge: Create Panel of Plots

Plot AirTempMonthly and AirTempDaily next to each other rather than stackedon top of each other.

Additional ggplot2 Resources

In this tutorial, we've covered the basics of ggplot. There are many great resources the cover refining ggplot figures. A few are below:

• ggplot2 Cheatsheet from Zev Ross: ggplot2 Cheatsheet
• ggplot2 documentation index: ggplot2 Documentation

R Plots Not Showing Random